Objective

This lab focuses on gaining experience with PID control.

Prelab

Bluetooth communication setup for debugging

I implemented several BLE commands to make debugging and transmitting data over Bluetooth easier. My SET_GAINS command changes control gains without reprogramming the Artemis. My START_CONTROL and STOP_CONTROL commands raise flags that the robot continuously checks for; this allows me to start/stop the robot without having to “chase it down”.

Similar to previous labs, I let the robot continuously measure data in its loop() function and store it in arrays. After a run, I use my send_data command to transmit the stored data to my laptop.

Lab Tasks

PID control

In each iteration of the loop() function, my robot measures data and computes new PID values using a compute_PID() function I implemented.

The compute_PID function is shown below. [I forgot to upload this code snippet when the lab report was due. I understand that points will probably still be taken off, but I did want to clarify that I implemented this function before the lab was due.]

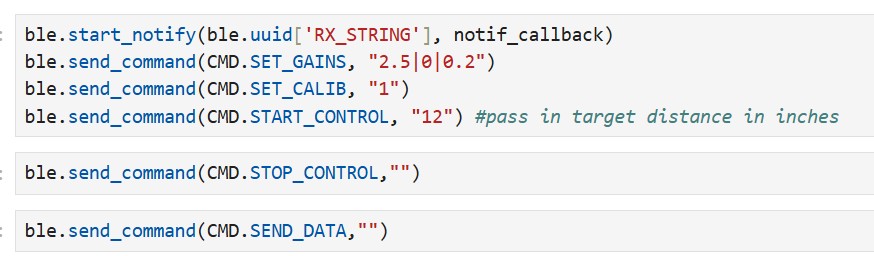
I set my PID gains to keep the PWM signal between 40 (the deadband from my previous lab) and 255 (the upper limit). Testing was done 6 feet from a wall, meaning the maximum error was 60 inches. This limited the maximum possible P-gain to 4.25. Initially, I used a P-controller with Kp = 2.9, but it resulted in over 10% overshoot, which I found unacceptable.

After tuning, I made several observations: a large proportional term causes overshoot, the derivative term is extremely noisy, and the integral term has little effect unless its gain is large.

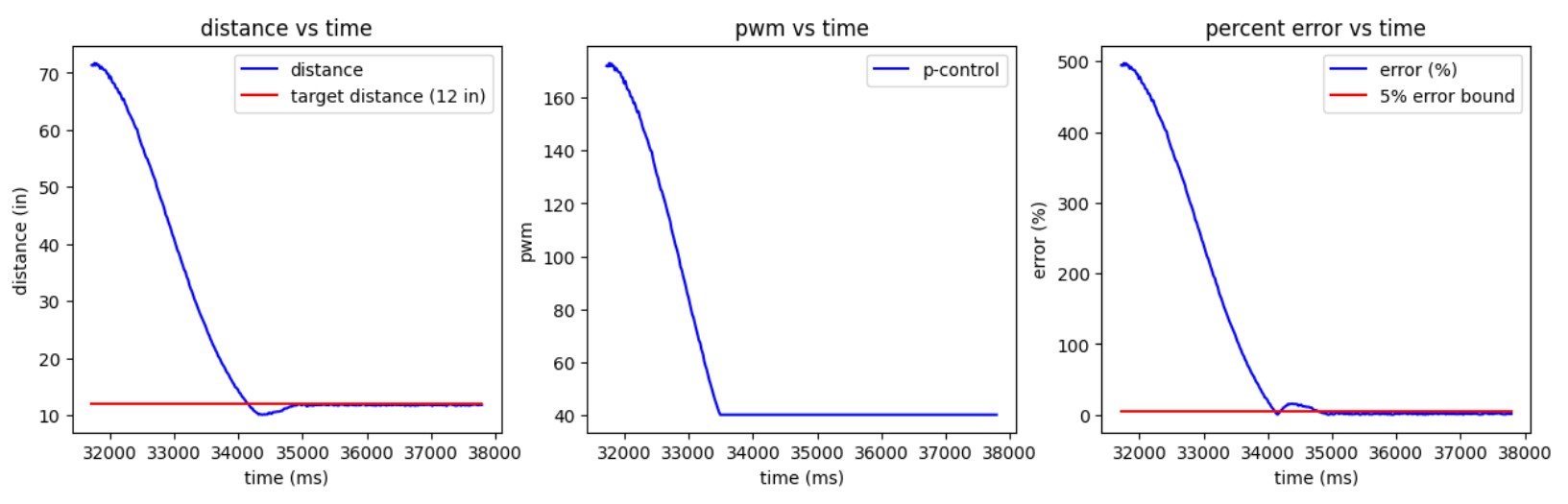
I implemented a low-pass filter for derivative control. By performing a DFT on a sample of derivative data, I determined a cutoff frequency of ~1.5–2 Hz. The two best-performing controllers were a PID controller with Kp = 2.5, Ki = 1, and Kd = 0.1, and a PD controller with Kp = 2.5, Ki = 0, and Kd = 0.2.

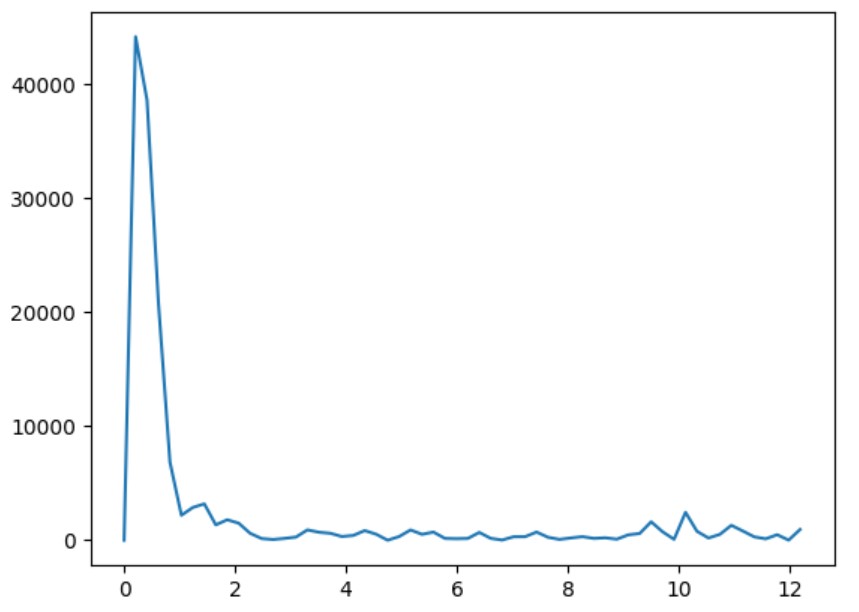
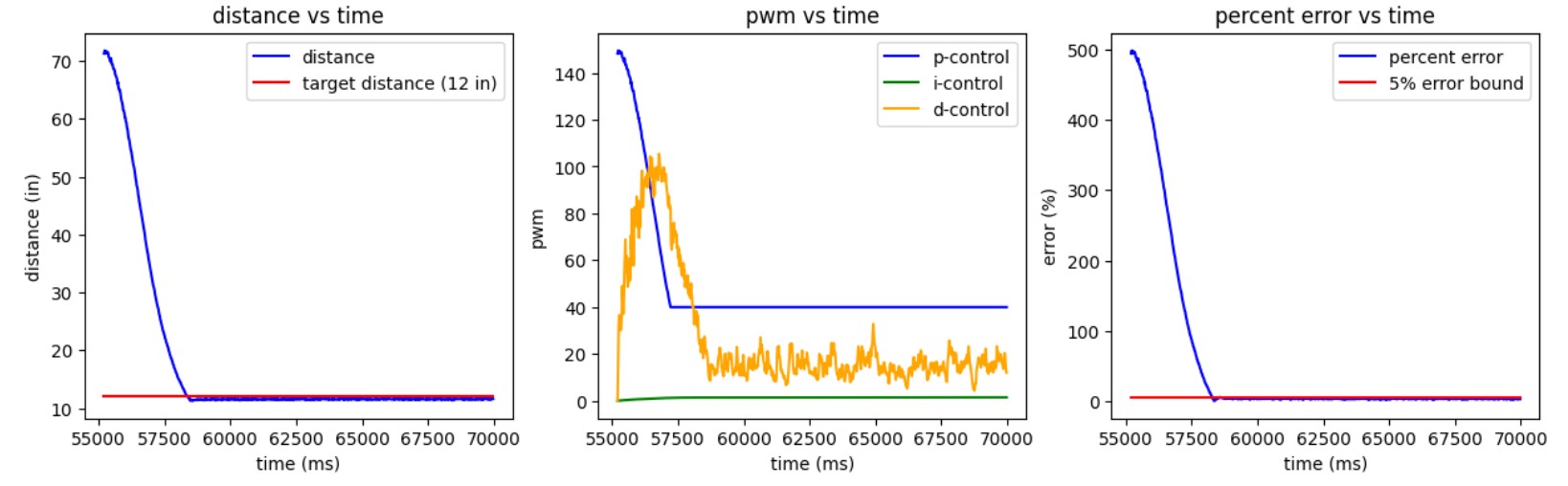
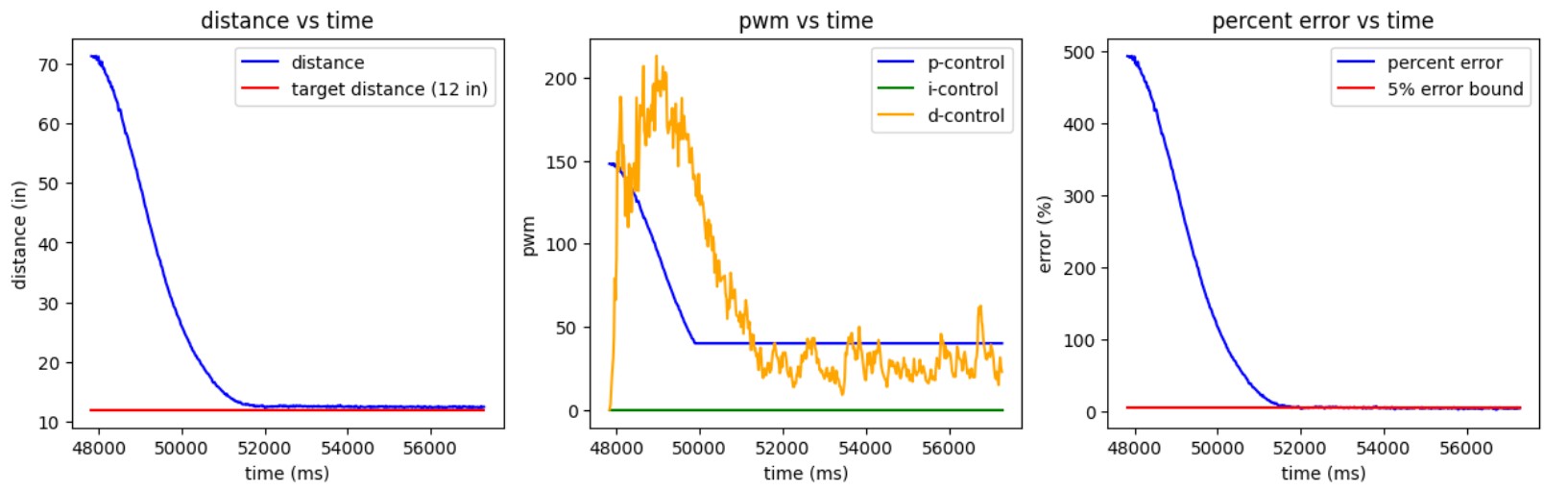
I liked these controllers because they had minimal overshoot and very low steady-state error. However, the robot moves slowly at 0.69 m/s, so I plan to tune it further for higher speed. Additionally, I only tested one starting distance—longer ranges may require adjustments. Moving forward, I may use only the PD controller to avoid integral wind-up.

Extrapolation, range, and frequency

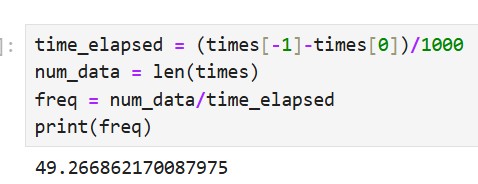
I used the ToF’s short-range mode; according to the datasheet, the ToF’s short-range mode performs best under ambient light conditions. Since the robot operates in such conditions, this was the optimal choice. To maximize sampling speed, I set the timing budget to 20 ms, the lower limit, allowing the sensor to sample at 50 Hz. I verified this rate with the data I collected.

To speed up the loop, I moved my PID computation out of the if-block that checks if ToF data is ready. To compensate for loss of data, I extrapolated distance values using the following function:

I tested the extrapolation on a simple P-controller.

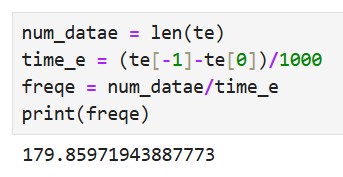
I was able to sample at a much higher rate, 180Hz, as shown below:

Discussion and acknowledgements

Acknowledgements

I worked with Rachel Arena on this lab.